How To Use Cyclomatic Complexity To Increase Test Coverage

Introduction

QA engineers write test cases to make sure that they do not skip any important use case and subsequently omit a bug. In case we don’t cover a specific testing path we are at risk of releasing a bug in production. This would lead to a higher bug fixing costs, general dissatisfaction of the client, loss of revenue and the brand reputation would suffer. I remember times when developers would add logic in the code which would have multiple if statements or loops. Of course, the logic for some of these statements would be used more than others. Without knowing all the possible paths where the code execution could traverse we cannot do the proper testing. The only question is how to find all the paths? How many of them are there? The answer is cyclomatic complexity.

What is Cyclomatic complexity?

In simple words, cyclomatic complexity is used for measuring the complexity of a piece of software. It is nothing new in the world of software development. It was first announced in 1976 by Thomas J. McCabe, Sr. in his article “A Complexity Measure”. It measures the number of independent paths through source code and can be even used to prove that the code is too complex for maintenance. It is represented by control flow diagram and in simplest possible case the complexity is 1. That happens when the source code doesn’t contain any control flow statement, like IF or WHILE. An oversimplification of it would be to say that for each control flow statement the complexity increases by 1. Let’s understand mathematically how to calculate the cyclomatic complexity. 

How to measure complexity?

The calculation of cyclomatic complexity is done using a pretty much simple formula: M = E – N + 2P. N represents number of nodes, E represents a number of edges and P is a number of connected components. Graphically we can show a simple control flow diagram for better understanding the above.

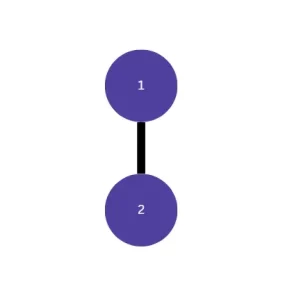
On the diagram the blue circles represent nodes (N), while black lines represent edges (E). There is only one connected component, meaning there is only one exit point. The formula would look like this M = 1 – 2 + (2*1). The result is 1. In case when there are no flow control expressions, the complexity would be 1. With each flow control expression we add to the code the complexity increases proportionally. The code for the graph above could look like this:

public string AddTwoNumbers(int firstNumber, int secondNumber) {
    return firstNumber + secondNumber;
}

If we create a method which prints out the age category based on age it would look like this:

public string PrintAgeCategory(int age) {
    string category = "minor";
    if(age >= 18) {
       category = "adult";
    } 
    return $"My age category is {category}";
}

In this case the diagram would look like this:

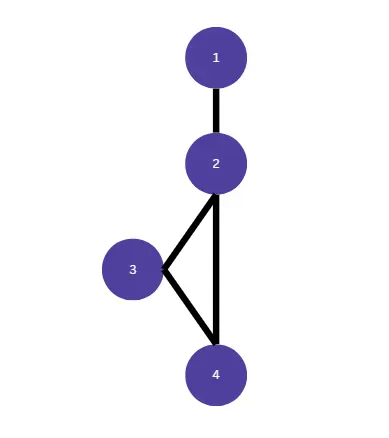
In this case the complexity is 2. If we use the formula then M = 4 – 4 + 2. The easiest way to calculate the complexity is to convert your code in graphical representation and use the formula then. It is not always so simple, especially in the case of nested conditional statements. McCabe provided us with some general guidelines on complexity. His remarks mention that a complexity under 10 is low complexity and easy to maintain and to understand. Complexity between 10 and 20 implies that there is a moderate risk in this function. If the complexity is between 20 and 50 then this is high complexity and high risk for maintenance. Complexity above 50 is untestable according to McCabe.

How to use Cyclomatic complexity to gain advantage in testing?

It is not unusual for me to go through the code of a commit when I start the testing of some feature. If the code is straight forward and concise I can understand to a certain extent its purpose. It gives me the idea of how should test the feature. If I see some conditional statements it will make me think about the possible paths where the execution could go to. In these situations usually it is too complex to imagine all the paths just be looking at the code. Therefore, I start drawing a small diagram where I note all the nodes, edges and connected components. When I gather all the information I can create test cases to cover all the edge cases.

What I can also see is high risk for code maintenance if the complexity is too high. Code that is difficult to maintain and it can contain a lot of bugs. This code is a good candidate for refactoring. The good thing about cyclomatic complexity is that there are a lot of tools which actually calculate the complexity for you. Tools for static code analysis like Sonar Qube can warn you if your code has too high complexity.

Conclusion

Cyclomatic complexity is useful metric both for developers and quality engineers. It can be used primarily for unit testing but also in exploratory testing. It is a good conversation subject between the developers and quality assurance team as part of strategy for simplifying testing efforts. The QA engineers use it extensively for finding the most problematic areas for testing because the higher the complexity the higher is the chance that some bugs are hiding in that piece of code. It can be quite complicated to calculate especially in more complex and nested conditional statements, therefore it might be useful to use some tools to calculate it.